Superposition
[Notes]
Neuron activations have a privileged basis. The residual stream does not. This is because the nonlinearities are applied to the activations on an element-wise basis, which means that representing the non-linear computation under a change of basis gets messy and results in the element-wise computation no longer acting on elements independently. Another way of thinking about this is that the residual stream is rotation-independent because all interventions (reading/writing) to it are done via linear maps. Multiplying the writes by some rotation matrix \(R\) and the reads by some rotation matrix \(R^{-1}\) will leave the info & computation done by the stream unchanged. IIRC this is also empirically shown in the grokking paper, where the algorithm is found up to rotation.
It seems that features is just the term we use to represent the units of a transformer’s ontology. Alternative definitions include “a property of an input to a model, or some subset of it” (Neel) or “[a] scalar function of the input” (Chris Olah). Sometimes ‘meaningful feature’ is used to refer to features which are interpretable. However, Anthropic’s toy model of bottleneck superposition just takes a 5-dim input \(x\) and considers each dimension a feature in and of itself. This is more in line with Olah’s definition? Maybe this confusion will resolve itself with practice.
Superposition itself is the phenomenon where there model represents more features than dimensions. In the Toy Models paper, Anthropic found that when features are dense models learn something like PCA, in that the two most important features have orthogonal representations and the rest are not learned. But as sparsity increases, we have the following:
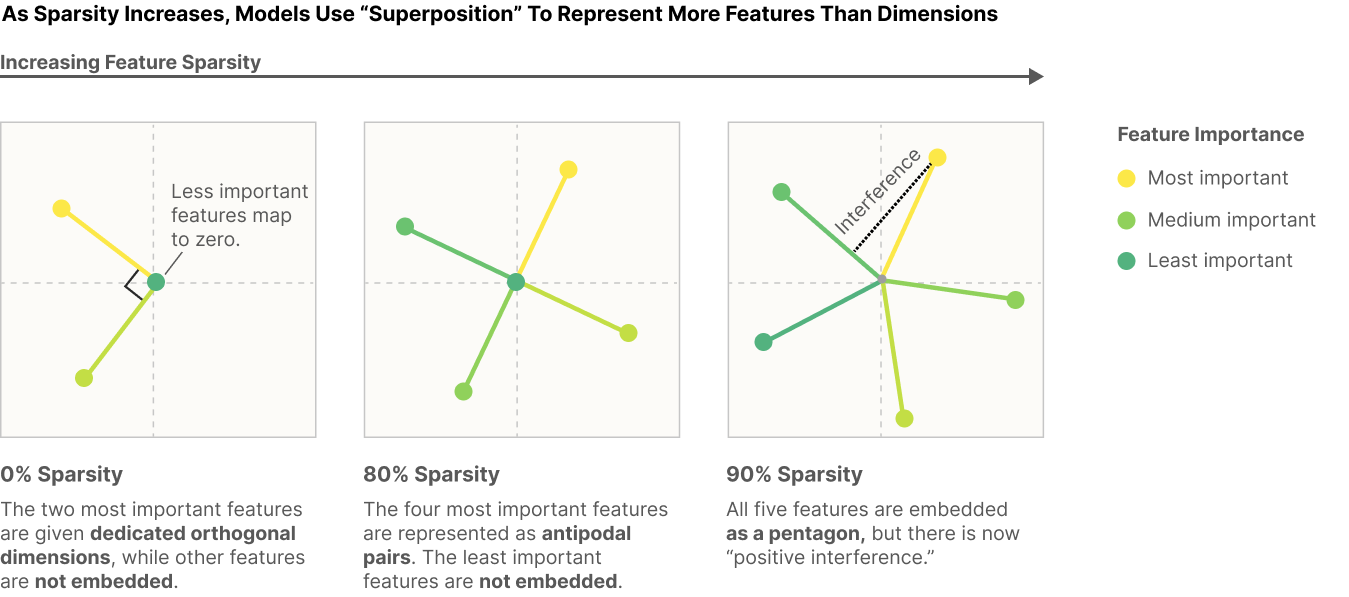
Sparsity here is defined as the probability of the corresponding element in \(x\) to the feature as being non-zero (e.g. is the feature represented in the input, roughly). We can also have different thresholds for sparsity that make sense, as in not nonzero but not above ~0.1. For instance, the second image has 80% sparsity because 4/5 of the features represented (and we assume that features are distributed evenly across the input set). In fact, it often makes sense (to me!) to think about sparsity as 1- feature probability rather than the other way around.
This is possible because sets of points in high-dimensional space can be embedded into a lower-dimension space in such a way that the distances between the points are nearly preserved by the Johnson-Lindenstrauss lemma. (I think this also implies that there can be exponentially many almost-orthogonal vectors in an n-dimensional space (exponential in the number of dimensions)).
Neel proposes two kinds of superposition: bottleneck superposition and neuron superposition:
- bottleneck superposition occurs in places like keys, queries, and the residual stream—places where a linear map goes from a large dimension to a relatively smaller dimension, and therefore information must be stored more efficiently/compactly
- neuron superposition occurs when dim(activation_space) < num_features, and is computation rather than storage. Computation occurs when info gets passed through nonlinearities, and n non-linearities attend to >n features in this case.
Consider a given neuron. A neuron is more likely to be polysemantic if the features it represents are sparse w.r.t. each other, and higher sparsity corresponds to more superposition in the general case. One reason we should expect superposition to be naturally occuring is that it will almost always make sense for networks to try to represent ever-more-sparse yet useful features, and these can be added to popular features at almost 0 cost.
Reading:
- Neel Nanda’s Notes on Superposition - good glossary and introduction
- Toy Models of Superposition - Anthropic’s first investigations into the subject
- 200 COP in MI: Exploring Polysemanticity and Superposition - some concrete open problems to do with superposition
- ARENA 1.4: Superposition and SAEs - great resource generally for hands-on learning
- Superposition, Memorization, and Double Descent - to replicate